ダイクストラのアルゴリズム - 例
ダイクストラのアルゴリズムは、負の重みを持たないグラフ内の源点と他のすべての頂点間の最短経路を探索するアルゴリズムです。
アルゴリズム
ダイクストラのアルゴリズムにまだ慣れていない場合は、まず例とその修正を見てください。アルゴリズムを最初に読むことは簡単ではありません。
関数: Dijkstra
入力:
- G = (A,S): 吸収サイクルのない有向グラフ。
- p: 2項関数
O(1)で辺の重みを与える
// 例 p(1,2) は辺(1,2)の重みを与える
- source: 始点のインデックス
出力:
- pred: 各頂点に対して選択された
前任者を含む配列。
- weight: 各頂点に対して
始点から到達するために渡る
合計重量(重みの合計)を含む配列。
開始:
// 初期化
For $s\in S$:
weight[s] <- inf
preds[s] <- "-"
EndFor
weight[source] <- 0
// 関数の主要部分
Q <- S
While $Q \neq \emptyset$:
// 最初にminQを探す
// 最初に確認する頂点
temp <- inf
minQ <- -1
For $q \in Q$:
If weight[q] < temp:
temp <- weight[q]
minQ <- q
EndIf
EndFor
Q <- Q - {minQ}
For each successor q' of q: // グラフが無向であれば隣接点
// 記録された距離が
// 先行者の距離より大きい場合
// + 辺の重み:
// q'の情報を更新する
If weight[q'] > weight[q] + p(q,q'):
weight[q'] <- weight[q] + p(q,q')
EndIf
EndFor
EndWhile
End
このアルゴリズムは正の重みを持つグラフにのみ適用されます!負の重みを含むグラフがある場合(負の重みのサイクルがない場合)、 ベルマン-フォードアルゴリズムを使用できます。
例
ここに2つの有向グラフ(digraphs)があります。
- これらのグラフにダイクストラのアルゴリズムを使用して、sからtへの最短経路を見つけることができますか?
- できる場合は、ダイクストラのアルゴリズムを使用して、sからtへの最短経路を決定してください。
例1:
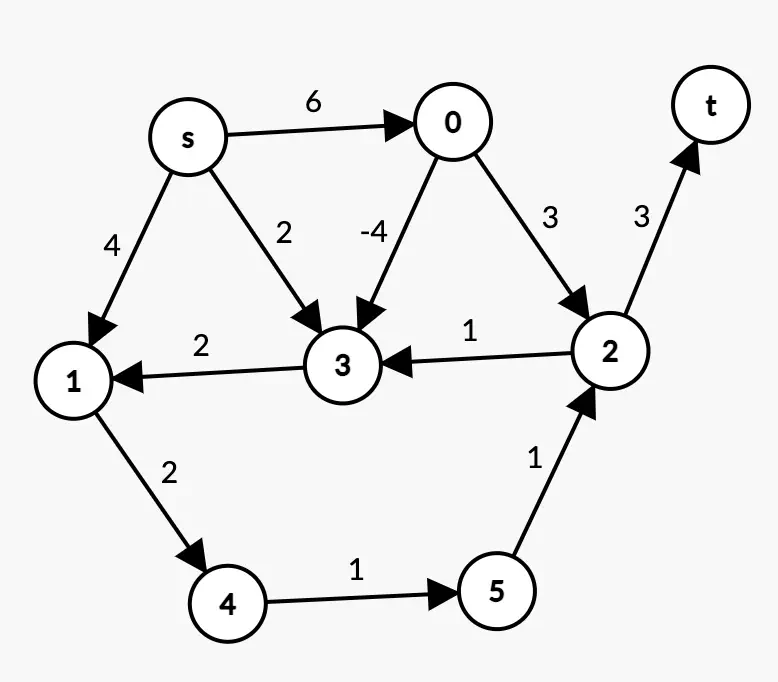
例1
例2:
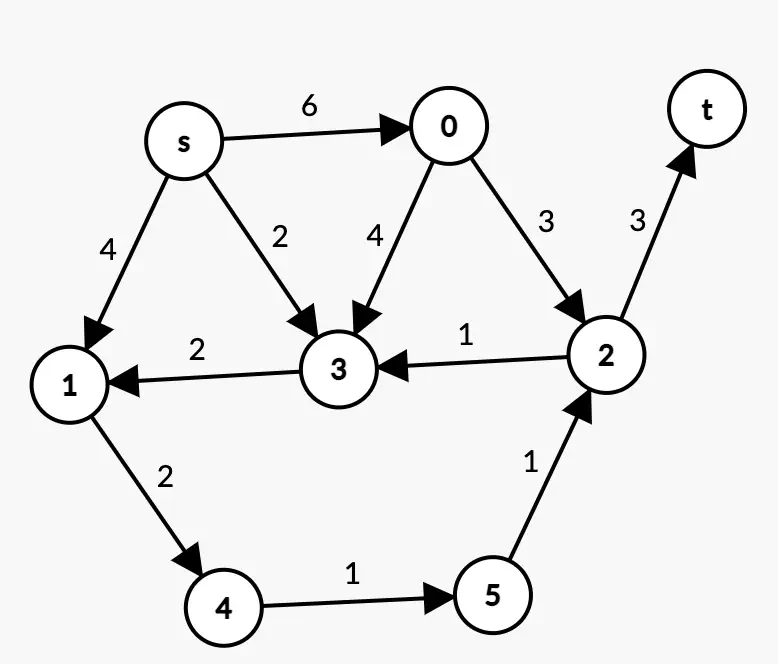
例2
解決策
解決策1
グラフの辺に負の重みが関連付けられています。したがって、ここではダイクストラのアルゴリズムは適用されません。代わりに ベルマン-フォードアルゴリズム(または別のアルゴリズム)を使用する必要があります。
解決策2
好みに合わせて2つのテーブルを組み合わせることができます。たとえば、各セルに「重み/先行者」を入れることができます。
重量表
| ステップ | s | 0 | 1 | 2 | 3 | 4 | 5 | t |
|---|---|---|---|---|---|---|---|---|
| 初期 | 0 | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ | $+\infty$ |
| Q -= s | / | 6 | 4 | $+\infty$ | 2 | $+\infty$ | $+\infty$ | $+\infty$ |
| Q -= 3 | / | 6 | 4 | $+\infty$ | / | $+\infty$ | $+\infty$ | $+\infty$ |
| Q -= 1 | / | 6 | / | $+\infty$ | / | 6 | $+\infty$ | $+\infty$ |
| Q -= 0 | / | / | / | 9 | / | 6 | $+\infty$ | $+\infty$ |
| Q -= 4 | / | / | / | 9 | / | / | 7 | $+\infty$ |
| Q -= 5 | / | / | / | 8 | / | / | / | $+\infty$ |
| Q -= 2 | / | / | / | / | / | / | / | 11 |
| Q -= t | / | / | / | / | / | / | / | / |
この表を理解するためのヒント:
- 各ステップで、最小の関連重みを持つ頂点を調べ、その後継者を検討します。たとえば、Q-=sのステップでは、sの後継者を見て、記録された値よりも近ければ、表を更新します。例えば、列0では:6<$+\infty$。
- “/“は読みやすさのためだけにあります。その上の数字がセルの実際の値です。
- Q -= sは、頂点sをQから削除することを意味します。アルゴリズムでのQの初期化を見ると、Q = “すべての頂点"があります。 各イテレーションで、Q内の頂点のみを扱うため、Q -= sのステップでは0の列を埋めます。
- Q -= 3では変更はありません。なぜなら3の後継者の中に1がありますが、weight[1] = 4はweight[3] + p(3,1) = 4に等しいからです。新しい重みが記録された重みよりも厳密に小さい場合のみ変更します。
- $Q -= 1$のステップの後、重量6の頂点が2つあります。選択は実際には重要ではありません。Qはセットであり、順序がないため、任意に辞書式の順序に従いましょう。
- 下の先行者テーブルは、頂点に到達するために取られた経路を追跡するのに役立ちます。2つのテーブルは同時に記入されます。
先行者テーブル
| ステップ | s | 0 | 1 | 2 | 3 | 4 | 5 | t |
|---|---|---|---|---|---|---|---|---|
| 初期 | - | - | - | - | - | - | - | - |
| Q -= s | / | s | s | - | s | - | - | - |
| Q -= 3 | / | s | s | - | / | - | - | - |
| Q -= 1 | / | s | / | - | / | 1 | - | - |
| Q -= 0 | / | / | / | 0 | / | 1 | - | - |
| Q -= 4 | / | / | / | 0 | / | / | 4 | - |
| Q -= 5 | / | / | / | 5 | / | / | / | - |
| Q -= 2 | / | / | / | / | / | / | / | 2 |
| Q -= t | / | / | / | / | / | / | / | / |
sからtへの最短経路を見つけましょう:
- tの先行者は2
- 2の先行者は5
- 5の先行者は4
- 4の先行者は1
- 1の先行者はt
したがって、sからtへの最短経路は:
$$s \rightarrow 1 \rightarrow 4 \rightarrow 5 \rightarrow 2 \rightarrow t$$
合計重量は:$4+2+1+1+3 = 11$