アルゴリズム
関数 : ベルマン-フォード
入力 :
- G = (V, E) : 負のサイクルを含まない有向グラフ
- p : 辺 (u, v) の重みを O(1) で返す2項関数
- s : V 内の始点のインデックス
出力 :
- prev : 各頂点の前の頂点を含む配列。
- weight : 各頂点に対し、始点からその頂点までの最短経路(重みの合計)の重みを含む配列。
開始 :
各 v に対して V :
weight[v] = 無限大
prev[v] = "-"
終了
weight[s] = 0 // 始点から始点までの最短経路の重みは 0
1 から |V| - 1 までの i について :
各辺 (u, v) について E :
もし weight[u] + p(u, v) < weight[v] ならば :
weight[v] = weight[u] + p(u, v)
prev[v] = u
終了
終了
終了
負のサイクルとは、合計重みが厳密に負であるサイクルのことを指します(例えば、最短経路の文脈で無限に重みを減少させるためにこのサイクルに無限に留まる必要があるようなサイクル)。
しかし、このアルゴリズムは負のサイクルの検出にも役立ちます。$|V| - 1$ 回の反復で、ベルマン-フォードは負のサイクルがない場合、始点から他のすべての頂点への最短経路を見つけるでしょう。その後に別の反復を行い、$prev$ が変更された場合、負のサイクルが存在することを意味します。
この記事ではアルゴリズムの複雑さや訂正については議論されていませんが、これらの情報はすべて Wikipediaページ で見つけることができます。
修正された演習
問題
次の有向グラフにベルマン-フォード アルゴリズムを適用して、始点 s から p への最短経路を見つけてください。
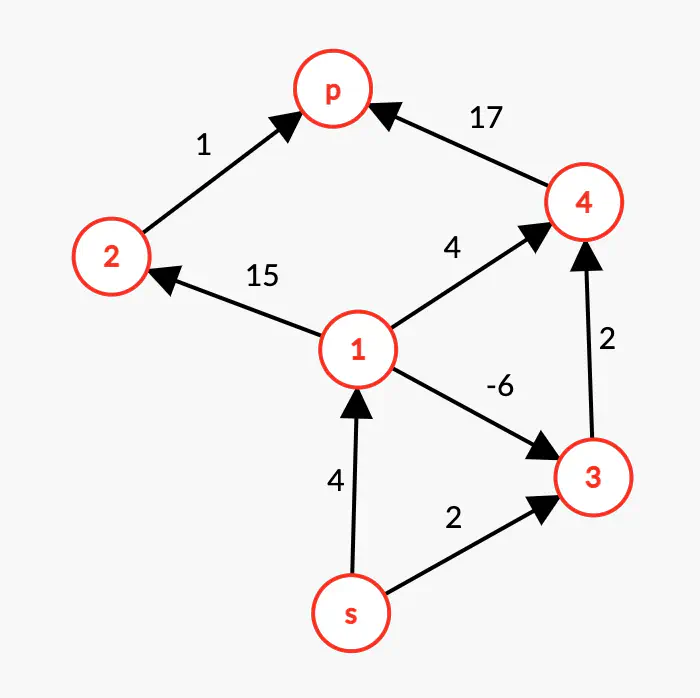
有向グラフ - ベルマン-フォード アルゴリズム
解答
重み表
| 反復 | s | 1 | 2 | 3 | 4 | p |
|---|---|---|---|---|---|---|
| 反復 0 | 0 | $\infty$ | $\infty$ | $\infty$ | $\infty$ | $\infty$ |
| 反復 1 | 0 | 4 | $\infty$ | 2 | $\infty$ | $\infty$ |
| 反復 2 | 0 | 4 | 19 | -2 | 4 | $\infty$ |
| 反復 3 | 0 | 4 | 19 | -2 | 0 | 17 |
| 反復 4 | 0 | 4 | 19 | -2 | 0 | 17 |
| 反復 5 | 0 | 4 | 19 | -2 | 0 | 17 |
このアルゴリズムには非決定論的な側面があります。 例えば 反復 2 の行を取ります。3の新しい重みが4の新しい重みより先に計算された場合、4の重みは0になり、4ではありません。アルゴリズムの実装(セット、リストなどを使用する)はこの順序を定義します。しかし、最後の行は誰にとっても同じであるはずです!
前の表
| 反復 | s | 1 | 2 | 3 | 4 | p |
|---|---|---|---|---|---|---|
| 反復 0 | - | - | - | - | - | - |
| 反復 1 | - | s | - | s | - | - |
| 反復 2 | - | s | 1 | 1 | 3 | - |
| 反復 3 | - | s | 1 | 1 | 3 | 4 |
| 反復 4 | - | s | 1 | 1 | 3 | 4 |
| 反復 5 | - | s | 1 | 1 | 3 | 4 |
$|V| - 1$ 回の反復でアルゴリズムを停止します。他のアルゴリズムの 実装 はこの数を減らすことができるかもしれません。
下から前の表を取ると、始点 s から p への最短経路は次のようになります:$$s \rightarrow 1 \rightarrow 3 \rightarrow 4 \rightarrow p$$
重みの合計は17です。