Différents types d'automates finis
Cet article présente un ensemble de propriétés concernant les automates finis. Pour mieux comprendre ces définitions, chaque type d'AFN sera illustré d'exemples générés grâce au logiciel Jflap. Les définitions formelles ne sont pas explicitées dans cet article mais sont disponibles via les liens sources.
Définitions :
Automate déterministe
Un automate est dit déterministe si il respecte trois conditions :
- Il possède un unique état initial.
- Il ne possède pas d’epsilon-transitions.
- Pour chaque état de cet automate, il existe au maximum une transition issue de cet état possédant le même symbole.
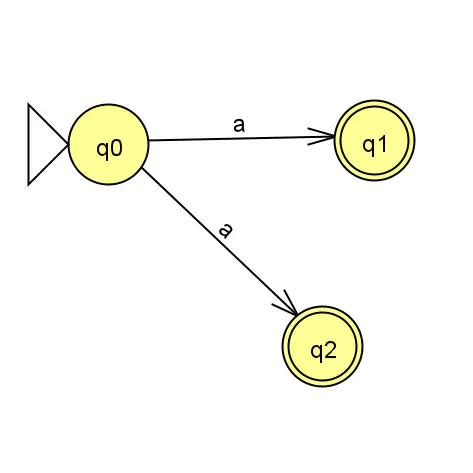
Pas un AFD
Attention : Un automate fini est toujours un AFN (automate fini non déterministe). Un automate fini déterministe (AFD) est un AFN particulier.
Automate complet
Un automate fini est dit complet si :
- Depuis n’importe quel état, tous les symboles de l’alphabet doivent appartenir au moins une fois aux transitions (sortantes).
Par exemple pour l’alphabet {a,b,c} :
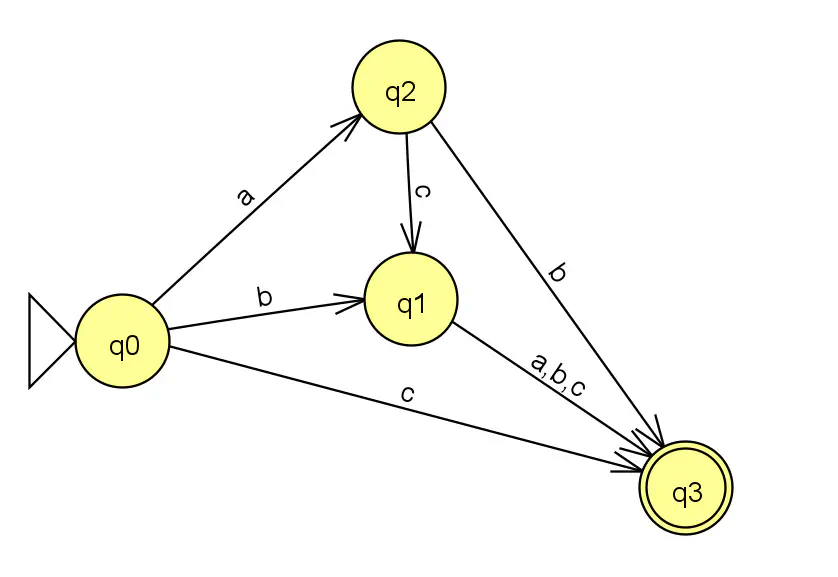
Automate fini non complet
Cet automate n’est pas complet car on ne peut pas obtenir le symbole “a” depuis q2.
Pour obtenir un automate équivalent, complet, il suffit de créer un état “puits”, ou état “poubelle”. Comme suit :
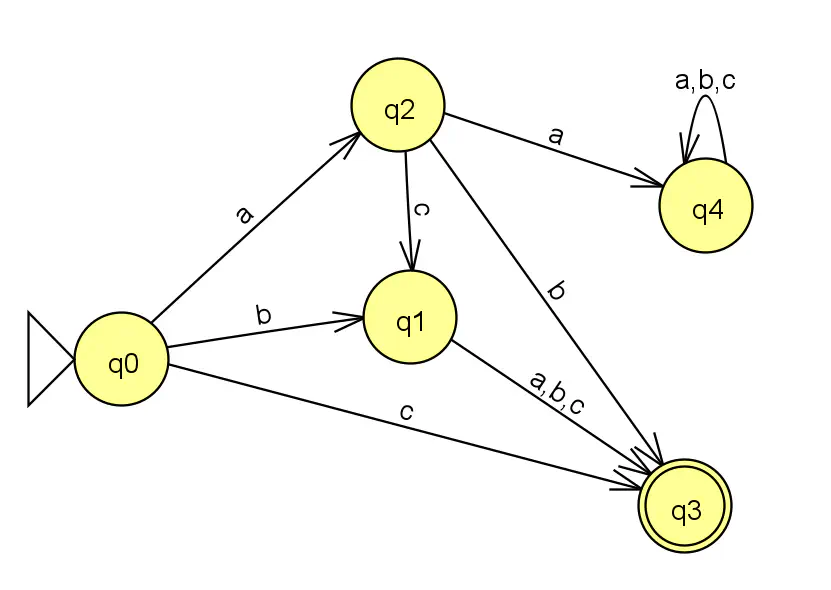
Automate fini complet
Automate émondé
Un automate est dit émondé (ou utile) si tous les états de cet automate peuvent former au moins un mot du langage.
Par exemple : Cet automate est fini émondé. q0, q1 et q3 peuvent servir tous les 3 à la création du langage.
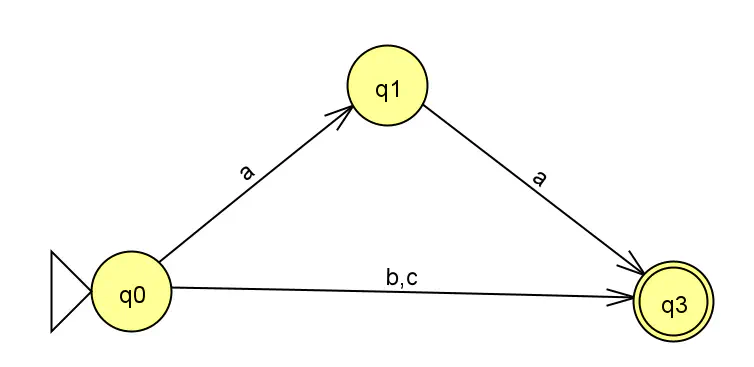
Automate fini émondé
Cependant celui là ne l’est pas : l’état q1 n’est plus “utile”.
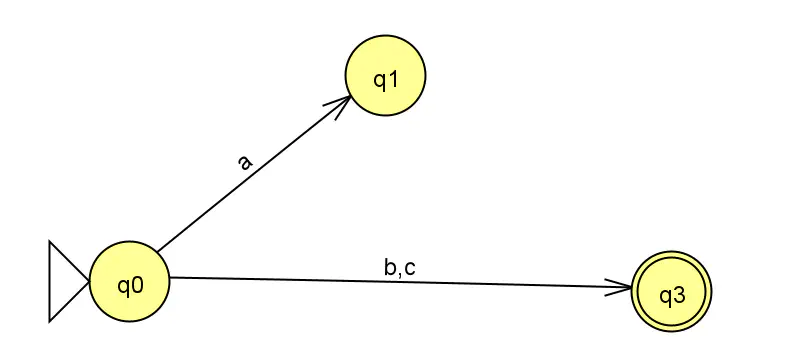
Automate non émondé
Automate unitaire
Un automate est dit unitaire si il possède un unique état initial.
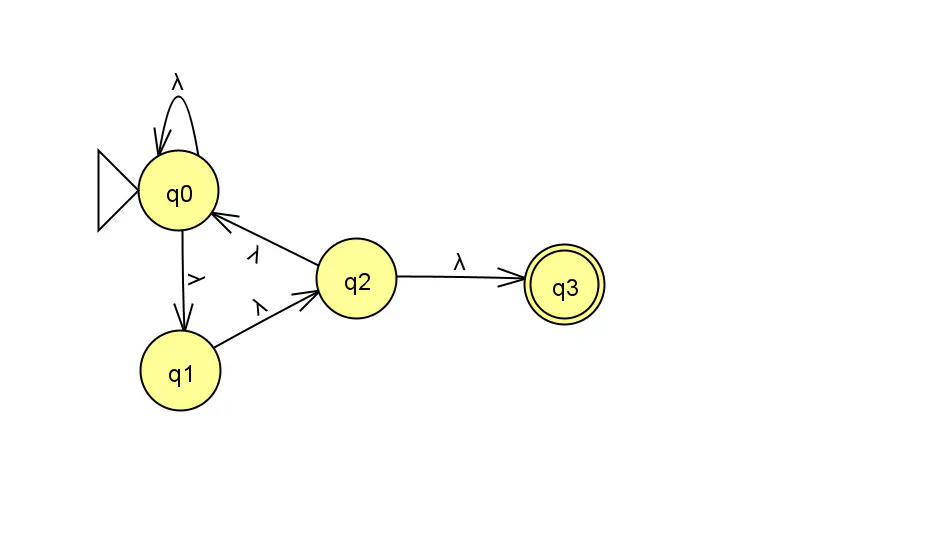
Automate unitaire
Automate standard
Un automate est dit standard si :
- Il est unitaire (un seul état initial)
- Il n’existe pas de transitions allant sur cet état initial
Par exemple, ceci n’est pas un automate standard :
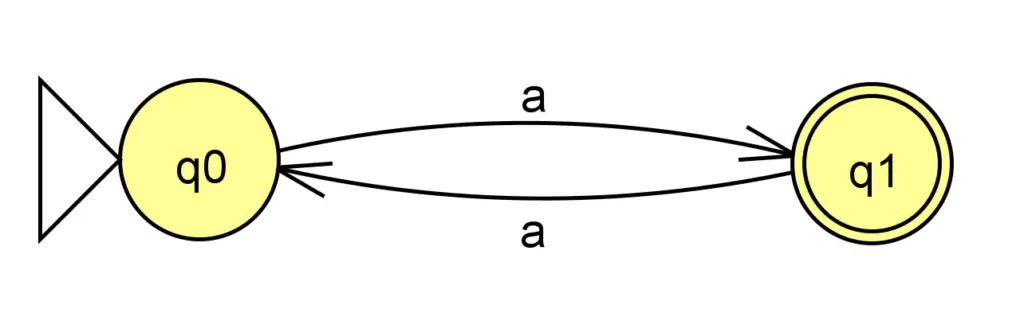
Automate non standard
Mais celui là l’est :
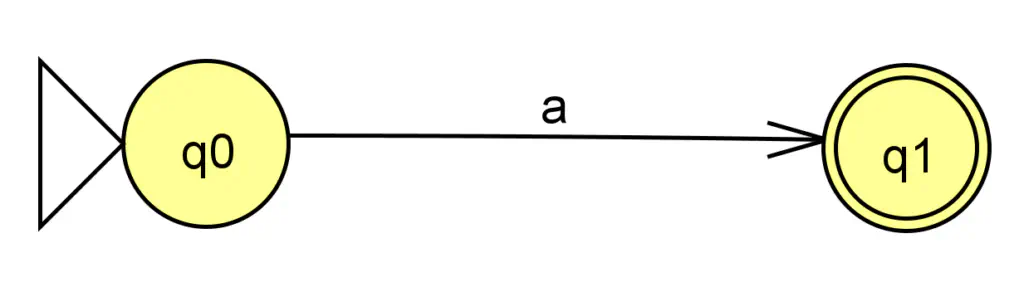
Automate standard
Automate normalisé
Un automate est dit normalisé si :
- Il est standard (aucune transition vers l’unique état initial).
- Il possède un unique état final
- Aucune transition n’a pour origine l’état final (on ne peut pas en sortir).
Par exemple cet automate n’est pas normalisé :
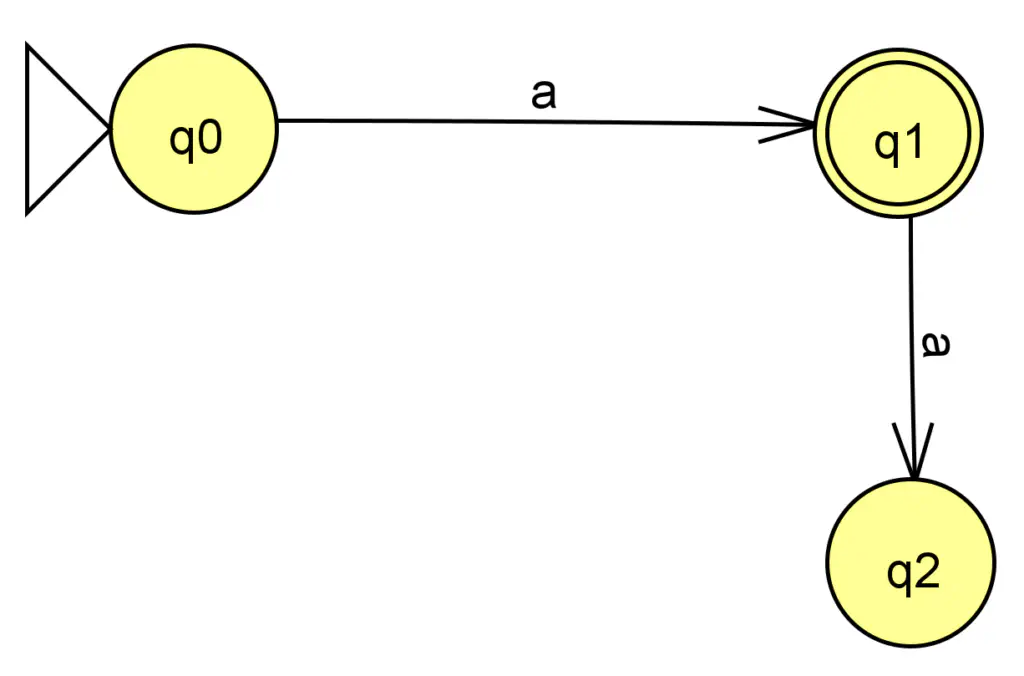
Automate non-normalisé
Cet automate est normalisé :
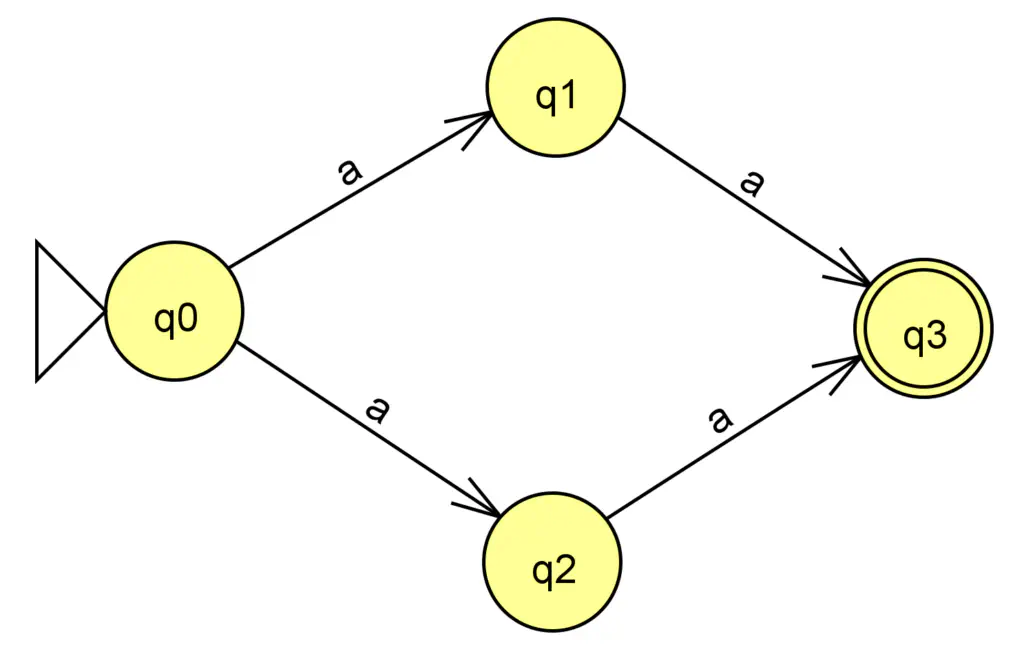
Automate normalisé