Parcours d'un arbre binaire

Différents parcours :

Commentaire : Par abus de langage, nous utiliserons le mot Arbre pour désigner une arborescence.

Soit Arbre, une structure telle que pour un arbre A:

A.e est l’élément du noeud de l’arbre
A.g est le fils gauche de A
A.d est le fils droit de A

Parcours préfixe

L’algorithme de parcours préfixe est le suivant :

    
        Procédure préfixe(Arbre A) : 
Début : 
   Afficher(A.e)
   Si A.g != null : 
      préfixe(A.g)
   FinSi
   Si A.d != null : 
      préfixe(A.d)
   FinSi
Fin

Parcours infixe

L’algorithme de parcours infixe est le suivant :

    
        Procédure infixe(Arbre A) : 
Début : 
   Si A.g != null : 
      infixe(A.g)
   FinSi
   Afficher(A.e)
   Si A.d != null : 
      infixe(A.d)
   FinSi
Fin

Parcours suffixe

L’algorithme de parcours suffixe est le suivant :

    
        Procédure suffixe(Arbre A) : 
   Si A.g != null : 
      suffixe(A.g)
   FinSi
   Si A.d != null : 
      suffixe(A.d)
   FinSi
   Afficher(A.e)

Parcours en largeur

L’algorithme de parcours en largeur est le suivant :

    
        Procédure largeur(Arbre A) : 
   Données : File-vide f, Arbre i
   Début : f.ajouter(A)
           Tantque (!f.estVide()) : 
              i = f.prendre()
              Afficher(i.e) 
              Si (i.g != null) : 
                 f.ajouter(i.g)
              FinSi
              Si (i.d != null) :
                 f.ajouter(i.d)
              FinSi
           FinTantque
   Fin

Exemple

Soit l’ABR suivant :

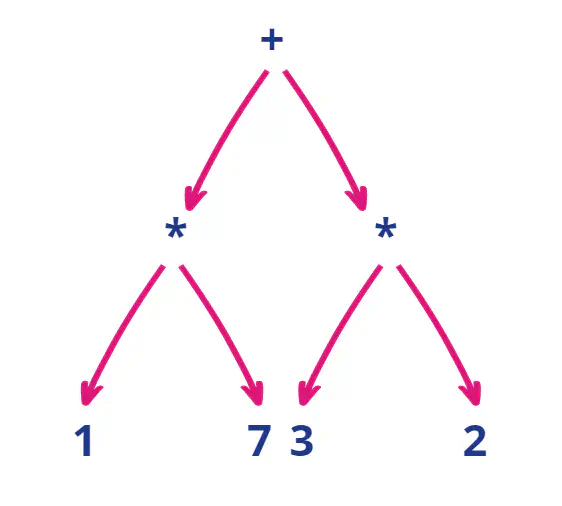
Exemple arbre binaire

Parcours préfixe : + * 1 7 * 3 2
Parcours suffixe ou postfixe : 1 7 * 3 2 * +
Parcours symétrique ou infixe : 1 * 7 + 3 * 2
Parcours en largeur : + * * 1 7 3 2

Commentaire :

Le résultat obtenu par le parcours suffixe de l’arbre binaire est similaire à la notion de “notation polonaise inversé” ou “notation post-fixé”, notamment utilisée dans le passé dans certaines calculatrices HP. Cette notation présentait plusieurs intérêts.

Si vous êtes intéressé pour en savoir plus, le sujet de la notation polonaise inverse est introduite dans cette vidéo de Computerphile :

mowse