Déterminisation d'un automate
Cet article présente une méthode afin de convertir un automate fini non déterministe quelconque (AFN) en automate déterministe (AFD). Afin d'illustrer cette méthode, un exercice corrigé sera utilisé comme support. Les étapes de l'algorithme de conversion seront explicitées de façon tabulaire.
Définition :
Un automate est dit déterministe s’il respecte trois conditions :
- Il possède un unique état initial.
- Il ne possède pas d’epsilon-transitions.
- Pour chaque état de cet automate, il existe au maximum une transition issue de cet état possédant le même symbole.
Pour en savoir plus : Différents types d’automates finis
Méthode :
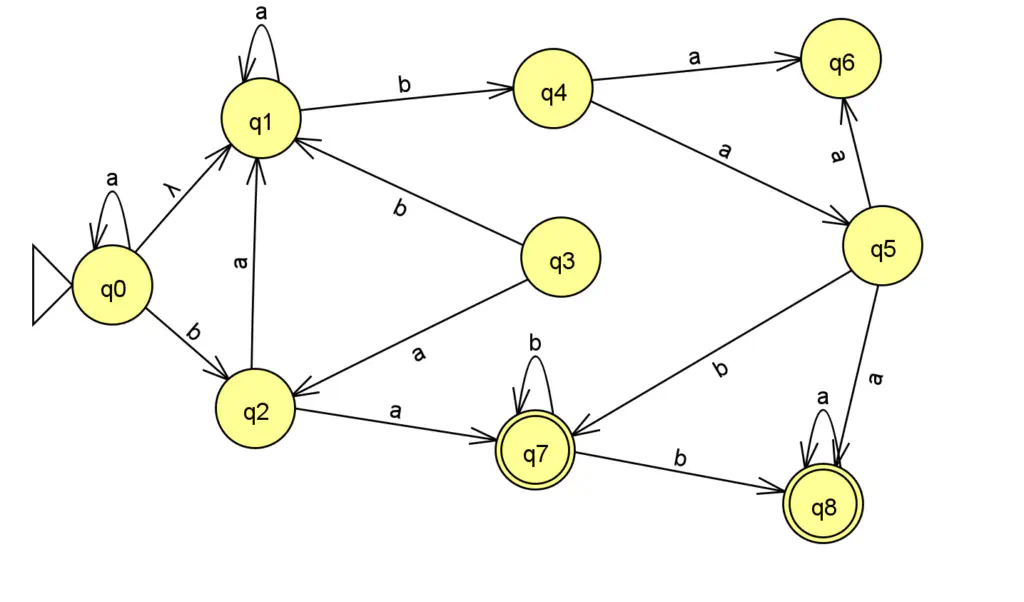
Automate fini non déterministe
La méthode permettant de passer d’un automate fini quelconque à un automate déterministe va être illustrée par l’exercice corrigé suivant :
Soit, un automate fini X sur l’alphabet {a,b} (le mot vide étant lambda) :
Calculons l’automate déterministe Y équivalent à X par la méthode des sous-ensembles d’états.
Étape 1 : Construction du tableau
Soit le tableau à 4 entrées suivant :
| Nouvel état | Nouvel état initial, final ou non | a | b |
Colonnes du tableau
- “Nouvel état” correspond au futur état de notre automate déterministe.
- “Nouvel état initial, final ou non” correspond au type de l’état de notre automate déterministe.
- Le reste des colonnes correspond aux symboles des transitions partant de ce nouvel état. Il y a autant de colonnes que le cardinal de l’alphabet de l’automate.
Commençons avec la première ligne :
| Nouvel état | Nouvel état initial, final ou non | a | b |
| A={q0, q1} | Initial | {q0,q1} = A | {q2,q4} = B |
| B={q2,q4} |
Colonnes du tableau
NB : Les noms des nouveaux états sont purement arbitraires.
1) Recherche de l’état initial :
L’état initial de X est q0. Une epsilon-transition de q0 vers q1 nous permet de réunir q0 et q1.
2) Initial ? Final ?
q0 est l’état initial de X, alors A contenant q0 le sera aussi. (c’est l’unique état initial)
A ne contient pas d’état final, il ne le sera donc pas lui-même.
3) Transitions ?
A partir de q0 ou de q1, il existe 2 transitions “a” se dirigeant vers q0, q1. Cet état existe. On s’arrête.
A partir de q0 ou de q1, il existe une transition “b” se dirigeant vers q2. Cet état n’existe pas, créons-le.
4) Répétons les étapes
A partir de ces nouveaux états, recommencer depuis l’étape 2 jusqu’à ce qu’il n’y ait plus de nouveaux états à être créés:
Résultat :
| Nouvel état | Nouvel état initial, final ou non | a | b |
| A={q0, q1} | Initial | {q0,q1} = A | {q2,q4} = B |
| B={q2,q4} | non | {q1,q5,q7} = C | Ø |
| C = {q1,q5,q7} | final | {q1,q8} = D | {q7,q4,q8} = E |
| D = {q1,q8} | final | {q1,q8} = D | {q4} = F |
| E = {q7,q4,q8} | final | {q5,q8} = G | {q7,q8} = H |
| F = {q4} | non | {q5} = I | Ø |
| G ={q5,q8} | final | {q8} = J | {q7} = K |
| H = {q7,q8} | final | {q8} = J | {q7,q8} = H |
| I = {q5} | non | {q8} = J | {q7}=k |
| J = {q8} | final | {q8} = J | Ø |
| K = {q7} | final | Ø | {q7,q8}=H |
q6 et q3 étant soit des états inaccessibles, soit des états stériles, ont été ignorés.
Étape 2 : Modélisation de l’automate à partir du tableau
Afin de tracer l’automate il nous suffit de créer des états de A à K, et de les relier en fonction de nos nouvelles transitions.
Vous devriez obtenir cet automate :
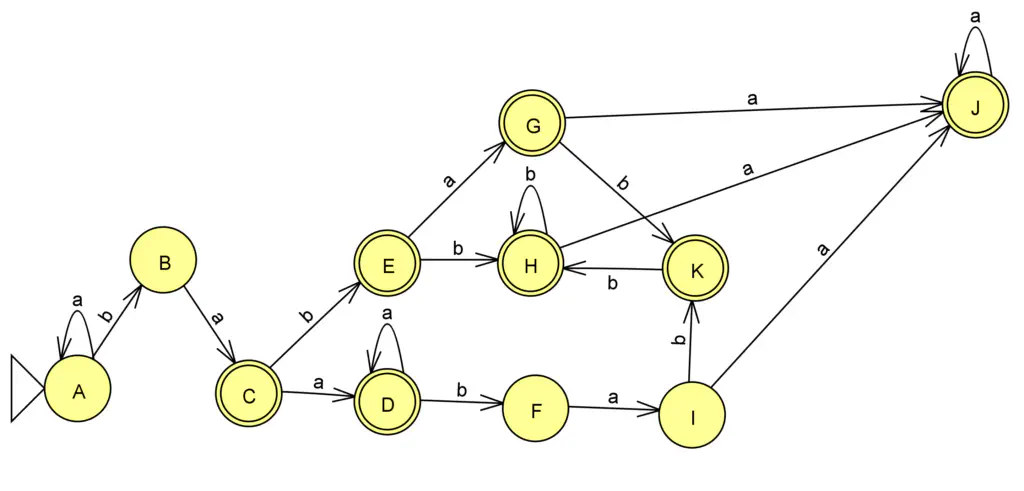
Automate équivalent déterministe