Algorithme de Bellman-Ford

L’algorithme

    
        Fonction : Bellman-Ford
Entrées : 
  - G = (A,S) : un digraphe sans cycle absorbant.
  - p : une fonction d'arité 2 
  donnant le poids d'un arc $\in O(1)$ 
  // Exemple p(1,2) donne le poid 
  de l'arc (1,2)
  - source : index du sommet source
  
Sorties : 
  - pred : Un tableau contenant 
  pour chaque sommet le sommet 
  précedant choisis.
  - poids : Un tableau contenant 
  pour chaque sommet le poids total 
  (la somme des poids) à parcourir 
  pour y acceder à partir de ori. 
	
Début : 
  Pour $s \in S$ : // Initialisation
    poids[s] <- Infini
    pred[u] <- "-"
  FinPour
 
  poids[source] <- 0 // De source à source, le poids est de 0
  
  Pour iter allant de 1 à $|S| - 1$ : 
    // Preuve de la condition d'arrêt sur wikipédia
    Pour $(u,v) \in A$ : //Chaque arc (u,v)
      Si poids[v] > poids[u] + p(u,v) : 
      // Si le poids enregistré est supérieur au 
      // poids du prédécesseur + poids de l'arc : 
      // On met à jour les informations de v
        poids[v] <- poids[u] + p(u,v)
        pred[v] <- u
      FinSi
    FinPour
  FinPour
Fin

Un circuit absorbant est un circuit ayant un poids total négatif (ie : un cycle qui, dans le contexte d’un plus cours chemin, nous imposerait de rester dans ce cycle infiniment pour réduire le poids infiniment.)
Cependant, cet algorithme peut permettre la détection de cycles absorbants. Au bout de la $|A| - 1$ itération, l’algorithme nous garantit le plus court chemin (si pas de circuit absorbant). Si nous effectuons un tour de boucle en plus et que le tableau $pred$ est modifié, cela signifie qu’il y a un circuit absorbant !

La complexité et la correction de l’algorithme ne sont pas discutées ici et ne sont pas le sujet de cet article. Vous pouvez cependant trouver toutes ces informations sur Wikipédia.

Exercice corrigé

Enoncé

Appliquez l’algorithme de Bellman-Ford sur le digraphe suivant pour déterminer le plus court chemin de s à p.

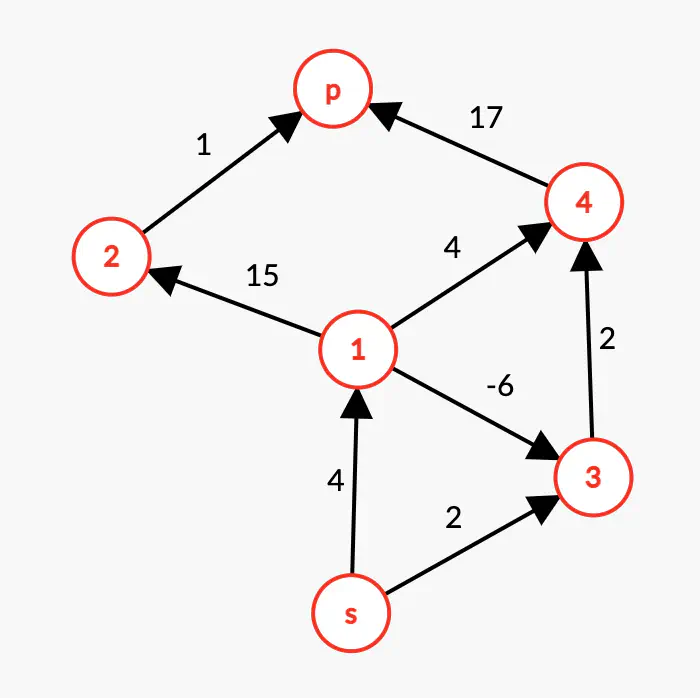
Digraphe - Algorithme de Bellman-Ford

Solution

Tableau des poids

Itération	1	2	3	4	p
Iter 0	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$
Iter 1	4	$\infty$	2	$\infty$	$\infty$
Iter 2	4	19	-2	4	$\infty$
Iter 3	4	19	-2	0	17
Iter 4	4	19	-2	0	17
Iter 5	4	19	-2	0	17

Il y a un aspect non déterministe dans cet algorithme. Prenons l’exemple de la ligne Iter 2. Si le nouveau poids de 3 est calculé avant le nouveau poids de 4, dans ce cas, le poids de 4 sera de 0 et non de 4. Cela dépendra donc de l’implémentation de l’algorithme (ensemble, liste, …). Ce tableau n’est donc pas unique, mais la dernière ligne devra être la même !

Tableau des prédécesseurs

Itération	s	1	2	3	4	p
Iter 0	-	-	-	-	-	-
Iter 1	-	s	-	s	-	-
Iter 2	-	s	1	1	3	-
Iter 3	-	s	1	1	3	4
Iter 4	-	s	1	1	3	4
Iter 5	-	s	1	1	3	4

Nous nous arrêtons à $|S|-1$ itérations. Des variantes de cet algorithme permettent de réduire ce nombre.

En reprenant le tableau des prédécesseurs à l’envers, nous avons pour plus court chemin de s à p : $$s \rightarrow 1 \rightarrow 3 \rightarrow 4 \rightarrow p$$

La somme des poids des arcs de ce sommet est de 17.

mowse

Algorithme de Bellman-Ford - Exemple