Example

For readability, episodes like $<A, B>$ are written as $AB$.

Yesterday, you monitored 4 activities that you have done for 7 hours.

The 4 events are the following:

• “M” : Listening to music
• “E” : Eating
• “S” : Sleeping
• “C” : Coding

Your day looked like the following:

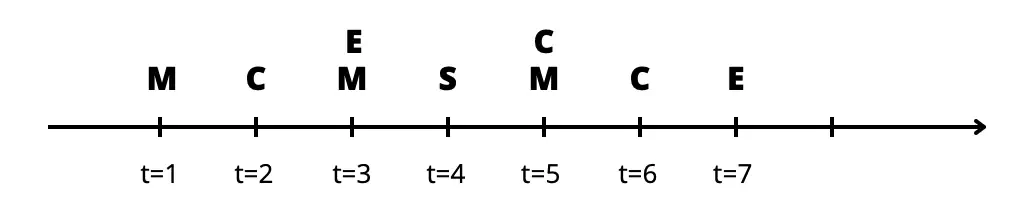
Minepi Example

With the MINEPI algorithm, try to identify the different episodes with the following constraints:

• $max_{span} = 3$ means that the maximum duration of an episode is 3 hours (3 hours means potentially 4 events).
• $min_{gap} = 1$ means that 2 events must be separated by at least 1 hour. Simultaneous events are not allowed.
• $min_{freq} = 2$ means that an episode must be present at least 2 times in the dataset.

Solution

Episodes of size 1

The first step is to identify frequent episodes of size 1. In our example, we have 4 events, so we have 4 episodes of size 1.

The candidate episodes of size 1 are:

$C_1 = \{M, E, S, C\}$

• $M$ is present 3 times: $id(M) = \{1, 3, 5\}$
• $E$ is present 2 times: $id(E) = \{3, 7\}$
• $S$ is present 1 time: $id(S) = \{4\}$
• $C$ is present 3 times: $id(C) = \{2, 5, 6\}$

Therefore, the frequent episodes of size 1 are: $F_1 = \{M, E, C\}$

Episodes of size 2

Starting here, we don’t have to look anymore at the sequence, we can just compute each frequency by looking at the size 1 results.

The candidates are, all the combinations of $M$, $E$ and $C$.

$C_2 = \{MM, ME, MC, EM, EC, CM, CE, CC\}$

• $MM$ is present 2 times: $id(MM) = \{(1, 3), (3, 5)\}$
• $ME$ is present 2 times: $id(ME) = \{(1, 3), (5, 7)\}$ (not $(3, 3)$ because $min_{gap} = 1$)
• $MC$ is present 3 times: $id(MC) = \{(1, 2), (3, 5), (5, 6)\}$
• $EM$ is present 1 time: $id(EM) = \{(3, 5)\}$
• $EC$ is present 1 time: $id(EC) = \{(3, 5)\}$
• $CM$ is present 1 time: $id(CM) = \{(2, 3)\}$
• $CE$ is present 2 times: $id(CE) = \{(2, 3), (6, 7)\}$
• $CC$ is present 2 times: $id(CC) = \{(2, 5), (5, 6)\}$

The frequent episodes of size 2 are:

$F_2 = \{MM, ME, MC, CE, CC\}$

Episodes of size 3

The candidate episodes of size 3 are:

$C_3 = \{MME, MMC, MCE, MCC, CCE\}$

Note that if $ME$ was not in $F_2$, having $MC$ and $CE$ would not have been sufficient to have $MCE$ in $C_3$.

• $MME$ is present 1 time: $id(MME) = \{(3,7)\}$
• $MMC$ is present 1 time: $id(MMC) = \{(3,6)\}$
• $MCE$ is present 2 times:$id(MCE) = \{(1,3), (5, 7)\}$
• $MCC$ is present 1 time: $id(MCC) = \{(3, 6)\}$
• $CCE$ is present 1 time: $id(CCE) = \{(5, 7)\}$

The last frequent episode of size 3 is:

$F_3 = \{MCE\}$

Episodes of size 4

They are no candidates for episodes of size 4.

Conclusion

The frequent episodes are:

$$\bigcup_{i=1}^3 F_i = \{M, E, C, MM, ME, MC, CE, CC, MCE\}$$

Source:

Mannila, Heikki et al. “Discovery of Frequent Episodes in Event Sequences.” Data Mining and Knowledge Discovery 1 (2004): 259-289.