Johnson's Algorithm - Example
Johnson's algorithm is an algorithm for finding the shortest path between every vertex in a graph, including those with negative weights.
Prerequisites
To understand the workings of Johnson’s algorithm, it’s necessary to be familiar with two other shortest path algorithms:
Idea of the Algorithm
- Adding a Vertex: We add a vertex $w$ to the graph $G$ along with $|V|$ edges connecting $w$ to each vertex of $G$.
- We use Bellman-Ford’s algorithm from $w$ towards all other vertices of $G$. $d(s)$ gives us the distance between $w$ and $s$. If Bellman-Ford detects a negative cycle, the algorithm stops.
- Removal of Vertex $w$: This vertex is no longer useful. Remove this vertex and all the edges added in step 1.
- Re-weighting the Edges of the Graph: For each edge $(u,v)$ in the graph, do: $p((u,v)) := p((u,v)) + d(u) - d(v)$.
- Calculating the Shortest Path: For each vertex in $G$, apply Dijkstra’s algorithm to determine the shortest path between all vertices.
It is important to note that the distances are not preserved. If for an edge, we had a weight of $-2$, the new weight will be $\geq 0$. However, this is not the point. Johnson’s algorithm gives us the shortest path from point $A$ to point $B$ “only”. If you need to retrieve the sum of the weights of this path, just return to the original graph and follow the path given by Johnson.
Algorithm / Solution / Complexity
This article only presents an example of the application of Johnson’s algorithm. However, you can easily find this information on the internet:
Example:
Let $G$ be a graph with negative weight edges.
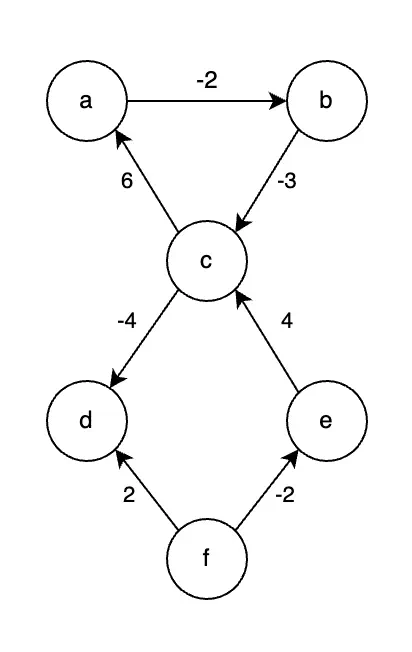
Initial Graph
Step 1 - Adding Vertex w
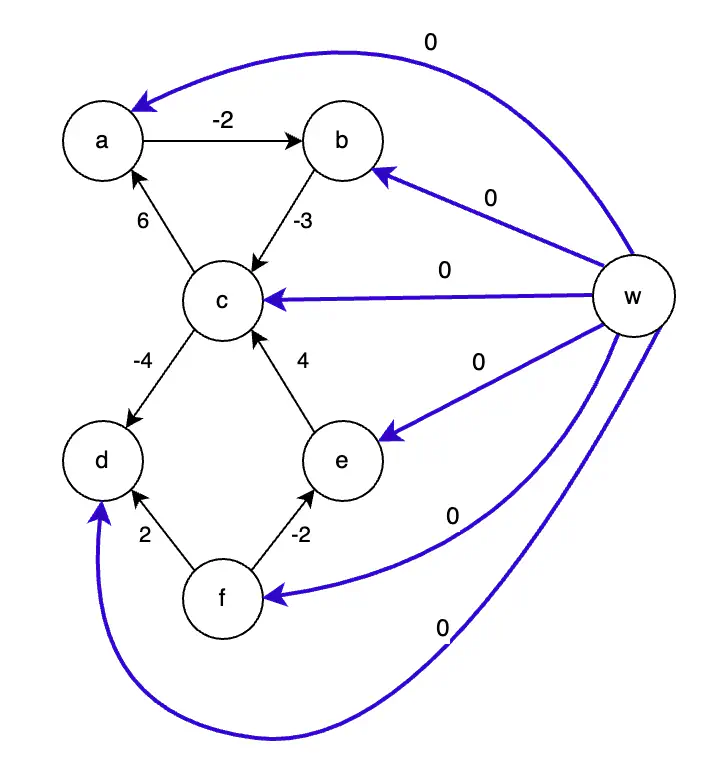
Adding w
Step 2 - Shortest Paths from w to Other Vertices Using Bellman-Ford
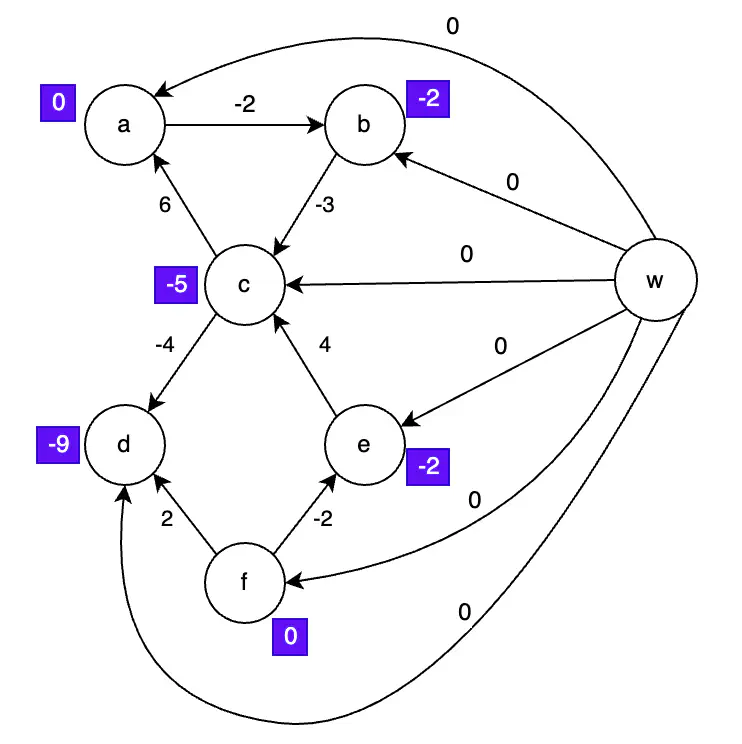
Shortest Paths Added
In purple are the results of Bellman-Ford’s algorithm.
Steps 3 and 4 - Re-weighting the Edges
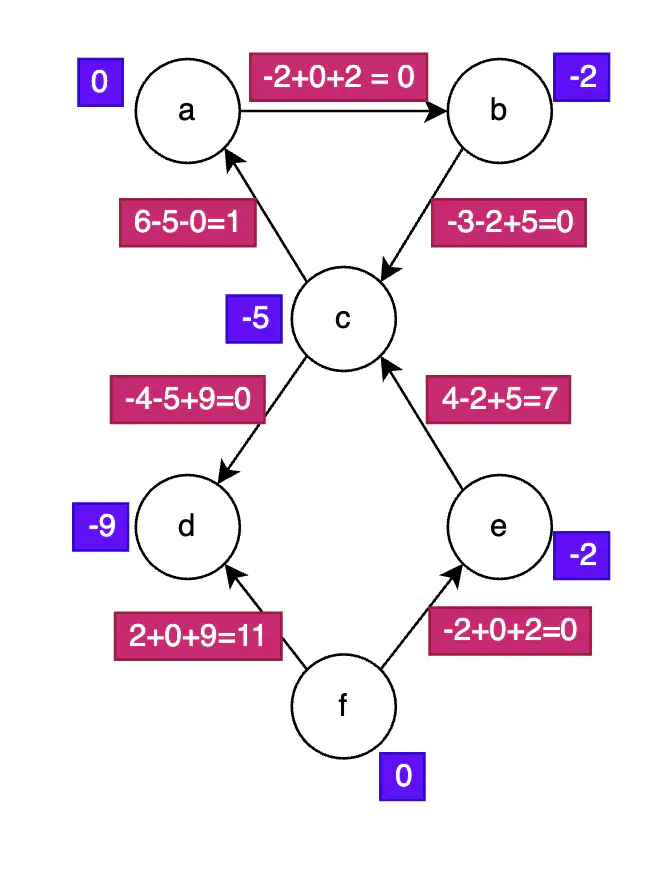
Re-weighting of Edges
Step 5 - Dijkstra’s Algorithm on All Edges
The final graph $G’$ is as follows:
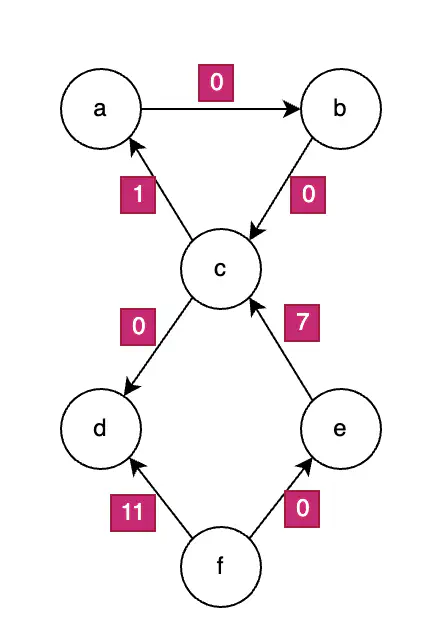
Graph G'
Step 5 is simply an application of Dijkstra’s algorithm. An example of its use is already detailed on this site: Dijkstra’s Algorithm - Example.
To take multiple results from Dijkstra’s algorithm:
- To go from a to d, the path to take is $a \rightarrow b \rightarrow c \rightarrow d$ with a weight of -9 (not 0, the weights from $G$ and not $G’$ must be used).
- To go from f to d, the path to take is $f \rightarrow e \rightarrow c \rightarrow d$ with a weight of -2.
- There is no possible path from d to e.
The rest is left as an exercise for the reader.