Bellman-Ford algorithm - Example
The Bellman-Ford algorithm is a shortest path algorithm for weighted digraph without negative cycles.
The algorithm
Function : Bellman-Ford
Inputs :
- G = (V, E) : a digraph without negative cycles
- p : an arity-2 function that returns the weight of the edge (u, v) in O(1)
- s : the index of the source vertex in V
Outputs :
- prev : An array containing the previous vertex of each vertex.
- weight : An array containing, for each vertex, the weight of the shortest path (sum of weights) from the source to this vertex.
Begin :
For v in V :
weight[v] = infinity
prev[v] = "-"
EndFor
weight[s] = 0 // The weight of the shortest path from the source to the source is 0
For i in 1 to |V| - 1 :
For each edge (u, v) in E :
If weight[u] + p(u, v) < weight[v] :
weight[v] = weight[u] + p(u, v)
prev[v] = u
EndFor
EndFor
End
A negative cycle is a cycle that has a total weight that is strictly negative (ie : a cycle that, in the context of a shortest path, would force us to stay in this cycle infinitely to reduce the weight infinitely).
However, this algorithm can help us in negative cycle detection. At $|V| - 1$ iterations, the Bellman-Ford, if there isn’t a negative cycle, will have found the shortest path from the source to all other vertices. If we then run another iteration and the $prev$ is changed, it means that there is a negative cycle.
The complexity or the algorithm correction is not discussed in the article, however, you can find all these informations in the Wikipedia page.
Corrected Exercise
Problem
Apply the Bellman-Ford algorithm to the following digraph to find the shortest path from the source s to p/
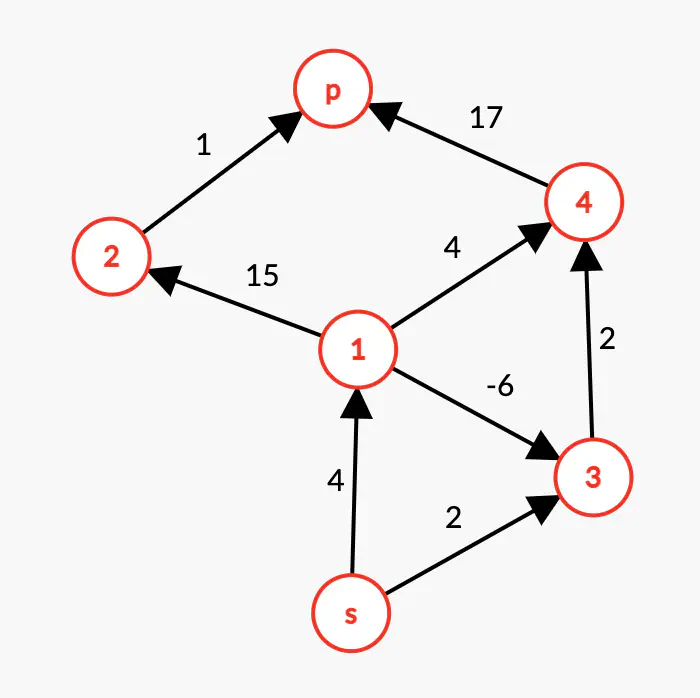
Digraphe - Algorithme de Bellman-Ford
Solution
Weight table
| Iteration | s | 1 | 2 | 3 | 4 | p |
|---|---|---|---|---|---|---|
| Iter 0 | 0 | $\infty$ | $\infty$ | $\infty$ | $\infty$ | $\infty$ |
| Iter 1 | 0 | 4 | $\infty$ | 2 | $\infty$ | $\infty$ |
| Iter 2 | 0 | 4 | 19 | -2 | 4 | $\infty$ |
| Iter 3 | 0 | 4 | 19 | -2 | 0 | 17 |
| Iter 4 | 0 | 4 | 19 | -2 | 0 | 17 |
| Iter 5 | 0 | 4 | 19 | -2 | 0 | 17 |
There is a non deterministic aspect in this algorithm. Take for exemple the line Iter 2. If new weight of 3 is computed begore the new weight of 4, then, the weight of 4 will be 0, and not 4. The algorithm implementation (using sets, list, …) will define this order. However, the last line should be the same for everyone !
Previous table
| Itération | s | 1 | 2 | 3 | 4 | p |
|---|---|---|---|---|---|---|
| Iter 0 | - | - | - | - | - | - |
| Iter 1 | - | s | - | s | - | - |
| Iter 2 | - | s | 1 | 1 | 3 | - |
| Iter 3 | - | s | 1 | 1 | 3 | 4 |
| Iter 4 | - | s | 1 | 1 | 3 | 4 |
| Iter 5 | - | s | 1 | 1 | 3 | 4 |
We stop the algorithm at $|V| - 1$ iterations. Other algorithm implementation could reduce this number.
By taking the previous table from the bottom, we have for the shortest path from s to p : $$s \rightarrow 1 \rightarrow 3 \rightarrow 4 \rightarrow p$$
The weighted sum is 17.